计算机图形学-2D到3D入门的入门

评论

背景/目标

这只是一个介绍性的分享, 目的在于让大家[自己]简单的了解 3D 画面是如何展现在画面上的

本次分享的内容, 大多数原理性内容来自于: GAMES101 闫令琪 的系列视频 2-6 集

注意: 本分享并没有介绍 OpenGL / WebGL / 渲染管线 的内容

线性代数推荐视频: https://www.bilibili.com/video/BV1ys411472E

需要的线性代数部分的知识

向量 / 矩阵的数学知识

向量

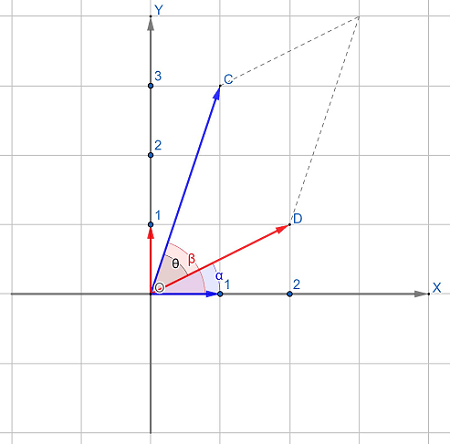
image

矩阵变换的性质

表示线性变换。所谓的线性变换，可以看成一种几何变换，把一个空间内的几何图形(点线面体)变换到另一个空间，它需要满足

  • 变换前是直线的，变换后依然是直线

  • 直线比例保持不变

  • 变换前的原点，变换后依然是原点

矩阵乘法

(m×n)(n×p) → (m×p) 一个 m×n 的矩阵 × 一个 n×p 的矩阵, 将会得到一个 m×n 的矩阵

img

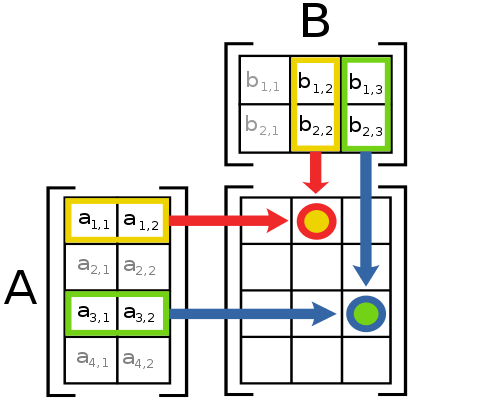
m = 3, n = 2, p = 4 → 3 × 4 的矩阵

怎么计算矩阵中的内容呢 ?

0, 0 位置的 9 怎么来的: 1 _ 3 + 3 _ 2 = 3 + 6 = 9

1, 0 位置的 19 怎么来的: 5 _ 3 + 2 _ 2 = 15 + 4 = 19

那么根绝规律发现, 如果想计算后矩阵的 第二行第一个[1, 0] 数字

左边的矩阵取第二行: 5 2, 右边的矩阵取第一列3 2, 然后逐个按顺序相乘并加起来

剩下的两个问号[?]位置也就根据上面这个规律来得出:

矩阵乘法的重要作用：

表示线性变换。所谓的线性变换，可以看成一种几何变换，把一个空间内的几何图形(点线面体)变换到另一个空间，它需要满足

  • 变换前是直线的，变换后依然是直线

  • 直线比例保持不变

  • 变换前的原点，变换后依然是原点

可以用线性变换来实现空间中的旋转、缩放、翻转等各种操作

我们可以用线性变换来实现空间中的旋转、缩放、翻转等各种操作

单位矩阵 Identity img
缩放 Scale img
翻转 Reflection img
旋转 Rotate 其中 img
斜切 Shear img

内容引自[有改动]: affine transformation

举个例子

将一个向量[列向量]缩放到 2 倍, 那么矩阵中的 S = 2, 现在有一个向量(3, 2)

m = 2, n = 2, p = 1 → 2 × 1 的矩阵

最终得到矩阵

问题?

矩阵变换好像不能表示平移

仿射变换 和 齐次坐标

内容引自: https://www.zhihu.com/question/20666664/answer/157400568

仿射变换

可以简单理解为 仿射变换 = 线性变换 + 平移

仿射变换带来的问题是: 非线性变换, 那么如何让平移变成线性变换?

齐次坐标 Homogeneous

将坐标系维度+1 在高一个维度使用线性变换来表示位移

img

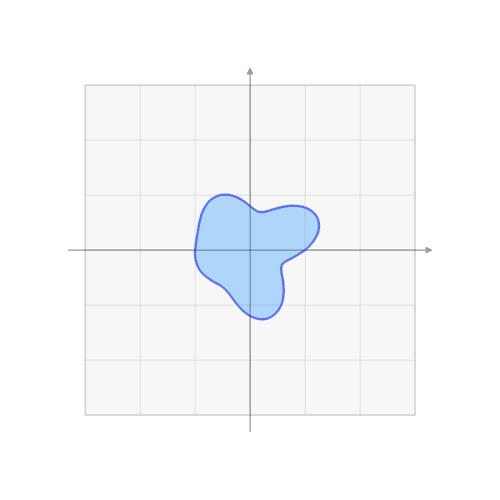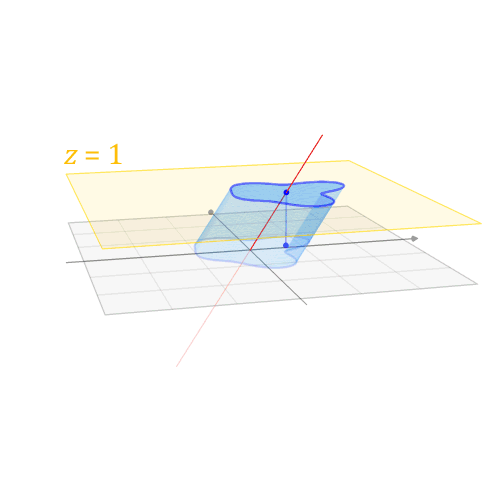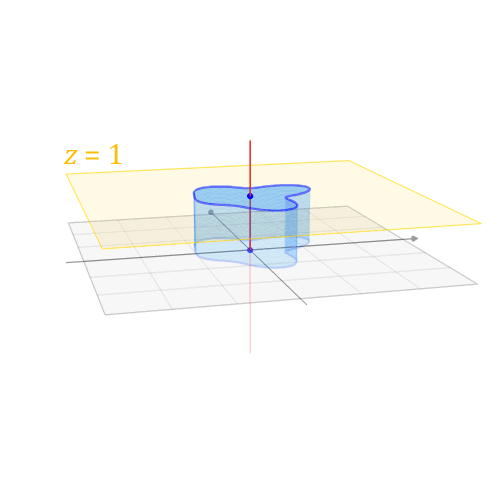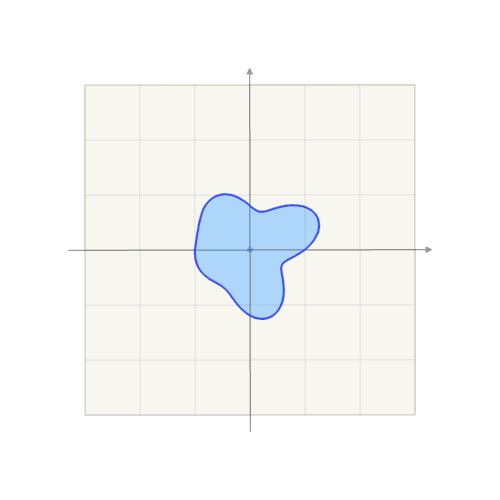
举个例子

我们希望将点(3, 2), x 和 y 分别移动+2 个位置得到 (5, 4)

首先我们将向量变为列向量, 并且维度+1 得到

加入一个单位矩阵将叫位移的距离分别填写在 x, y 的位置得到矩阵

计算

点乘

  • 找到两个向量的夹角
  • 找到向量的投影
  • 两个向量前与后的关系
  • 计算平行四边形/三角形的面积

叉乘

  • 两个向量左和右的关系
  • 判断一个点在凸边型内还是外
  • 得到一个和两个向量都垂直的向量

3D 模型是什么样的

如何表达一个 3d 模型

3d 模型文件[obj]中, 会哪些数据

1
2
3
4
5
6
7
8
9
10
11
12
v 0.085564 -0.187462 -0.081385
v 0.089373 -0.187462 -0.086563
v 0.089373 0.029356 -0.086563
vt 0.947243 0.538227
vt 0.947276 0.538227
vt 0.947276 0.543826
vn 0.8055 -0.0000 0.5926
vn 0.5925 0.0000 -0.8056
vn -0.5925 -0.0000 0.8056
f 1/1/1 2/2/1 3/3/1
f 5/5/2 6/6/2 7/7/2
f 8/8/3 7/7/3 2/2/3

v: 顶点

vt: UV 坐标

vn: 法线

f: 面, v/t/n 索引[顶点/uv/法线]

不依赖任何 OpenGL 和 WebGL 的情况下, 渲染一个 3D 模型

将顶点位置找出来, 并绘制

imgimgimg

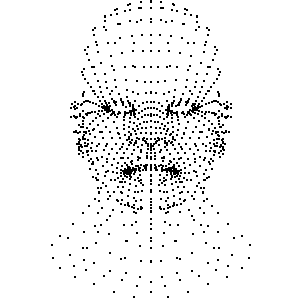
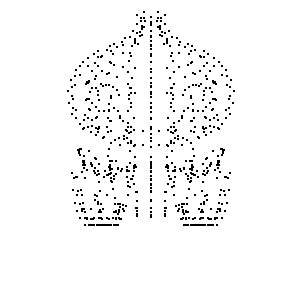
加入绕 Y 轴旋转

imgimgimg

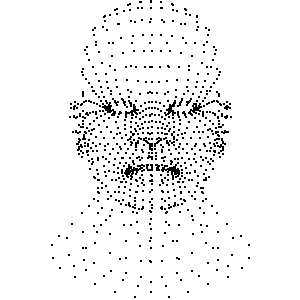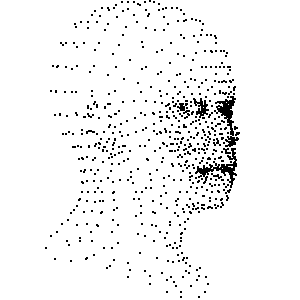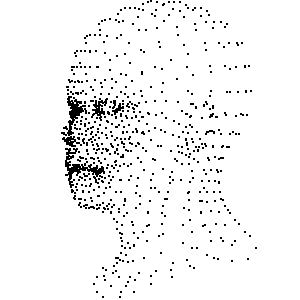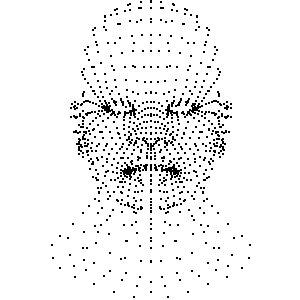
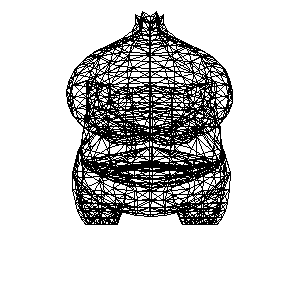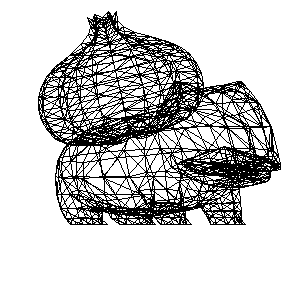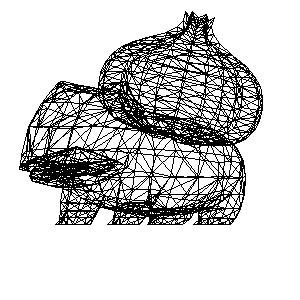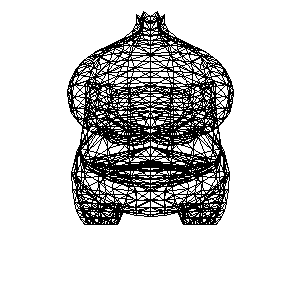
将[三角形]找出来, 将三角形相互连起来

imgimgimg

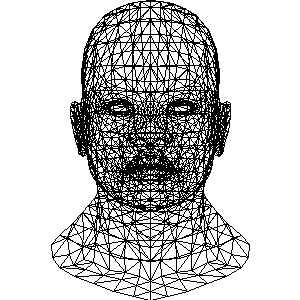
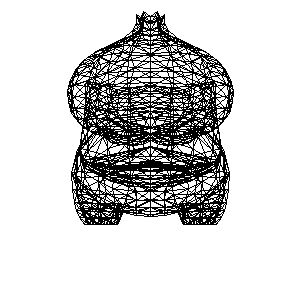
加入绕 Y 轴旋转

imgimgimg

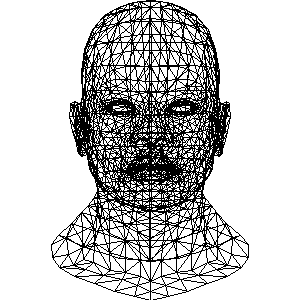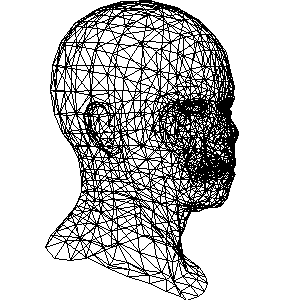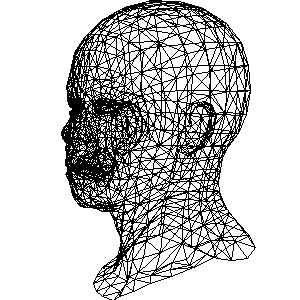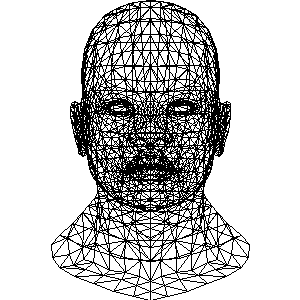
着色

UV 贴图

imgimgimgimg

模型中三角形和**UV**贴图的映射关系

截图来自Blender软件

imgimg

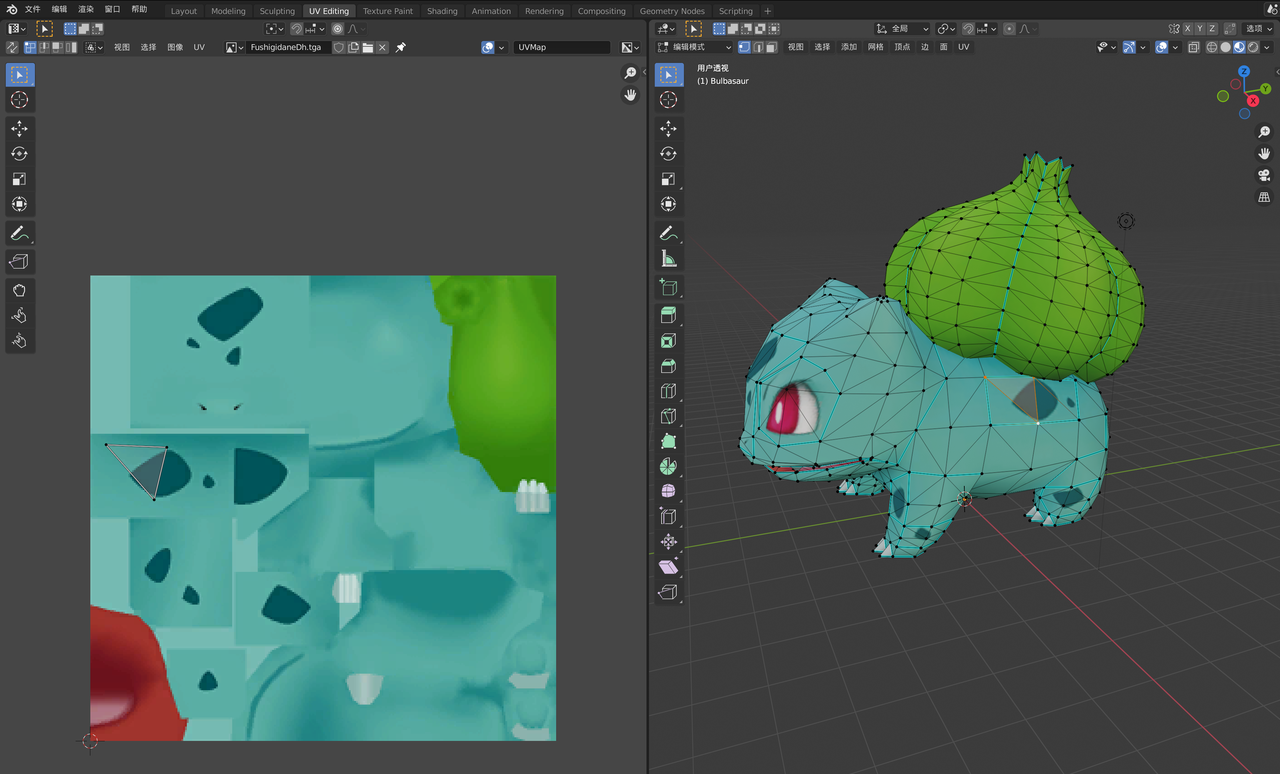
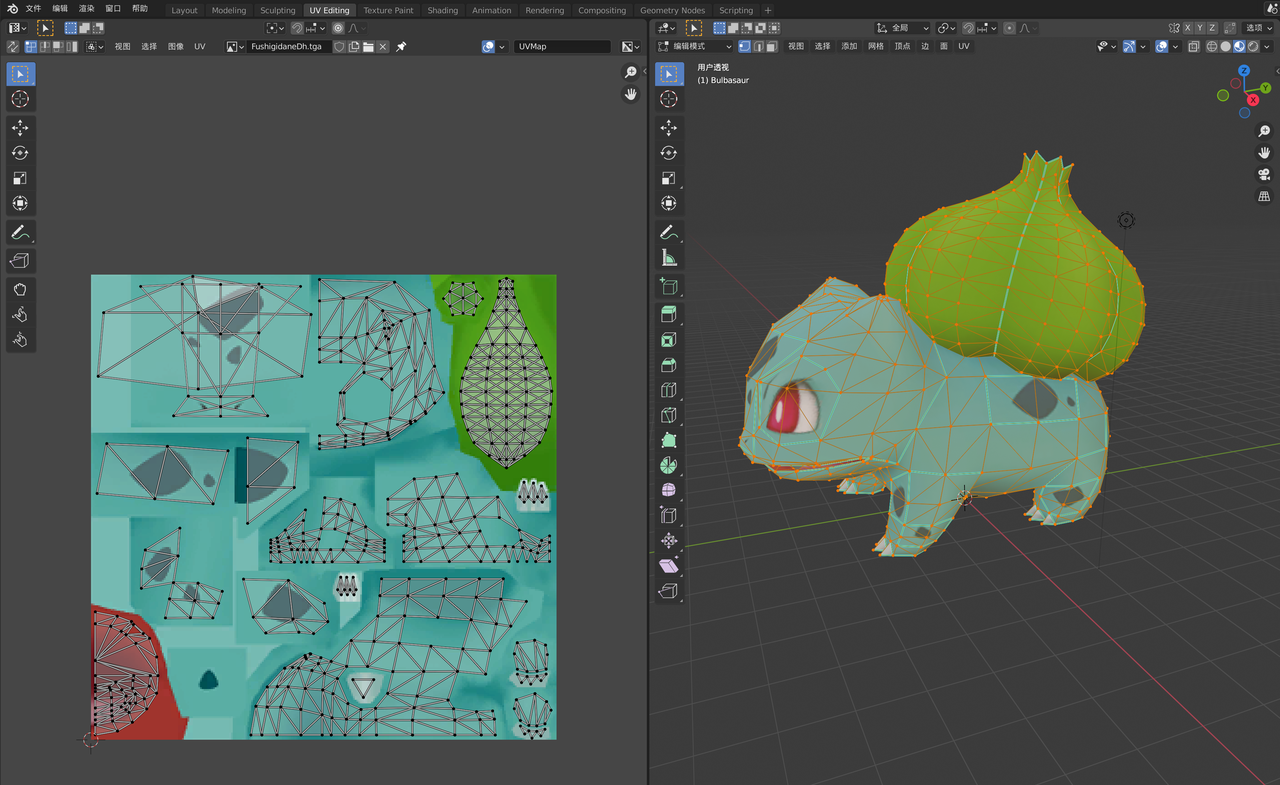
光栅化

img

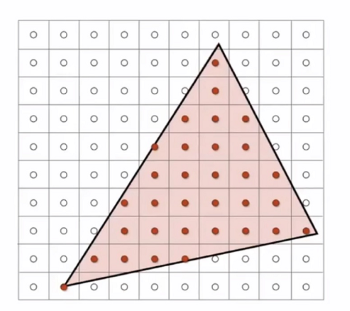
重心坐标 插值 / 判断内外[点是否在三角形内]

重心坐标, 不仅可以用来判断像素点是否在三角形内，还能利用这个重心坐标进行插值

img

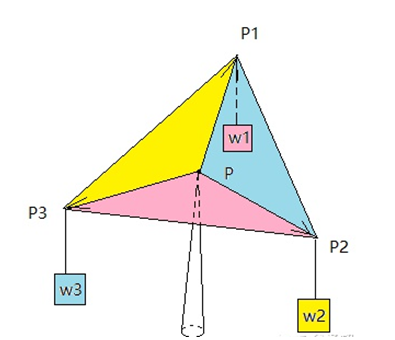
α = 粉红色的三角形面积 / 总面积 β = 黄色的小三角形面积 / 总面积 γ = 蓝色的小三角形面积 / 总面积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
x1, y1, x2, y2, x3, y3 = 三角形的三个顶点位置

cr1, cg1, cb1 := 255.0, 0.0, 0.0
cr2, cg2, cb2 := 0.0, 255.0, 0.0
cr3, cg3, cb3 := 0.0, 0.0, 255.0

for x := minX; x < maxX; x++ {
   for y := minY; y < maxY; y++ {
      a, b, c := ma.Barycentric(x1, y1, x2, y2, x3, y3, float64(x), float64(y))
      // 判断是否在三角形内
      if a < 0 || b < 0 || c < 0 {
         continue
      }
      // 对颜色进行插值
      rgba := color.RGBA{
         R: uint8(a*cr1 + b*cr2 + c*cr3),
         G: uint8(a*cg1 + b*cg2 + c*cg3),
         B: uint8(a*cb1 + b*cb2 + c*cb3),
         A: 255,
      }
      png.SetRGBA(x, y, rgba)
   }
}
img

深度测试[前与后的关系]

如果没有深度测试, 可能会导致后面的三角形渲染在前面, 如左图

imgimg

渲染结果

imgimgimg

imgimgimg

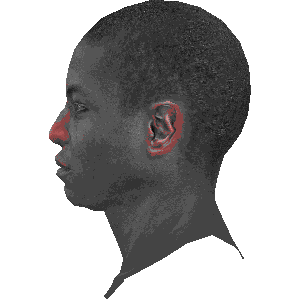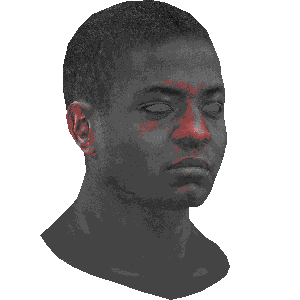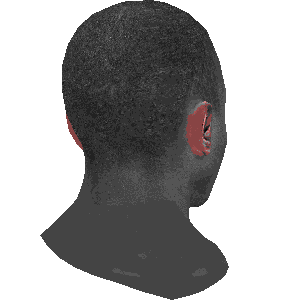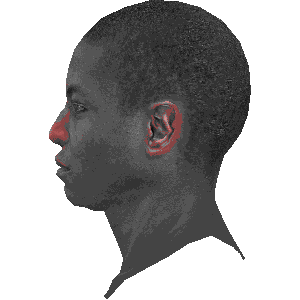
摄像机

模型可以自己旋转

也可以摄像机围绕着模型旋转

相对运动问题

img

imgimg

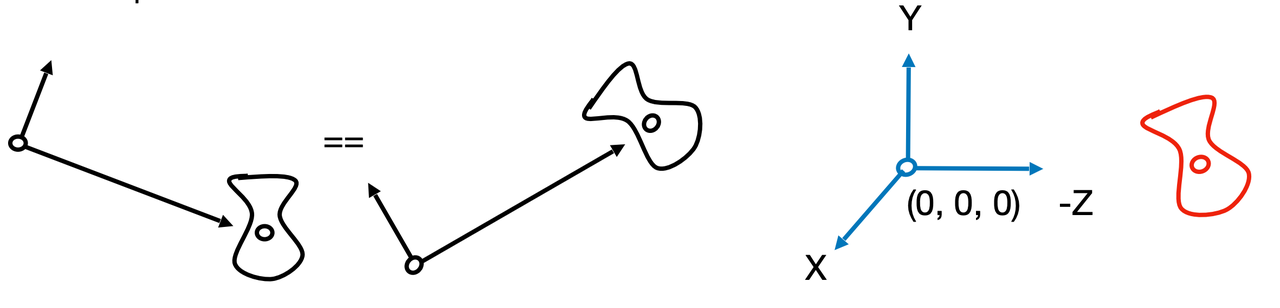
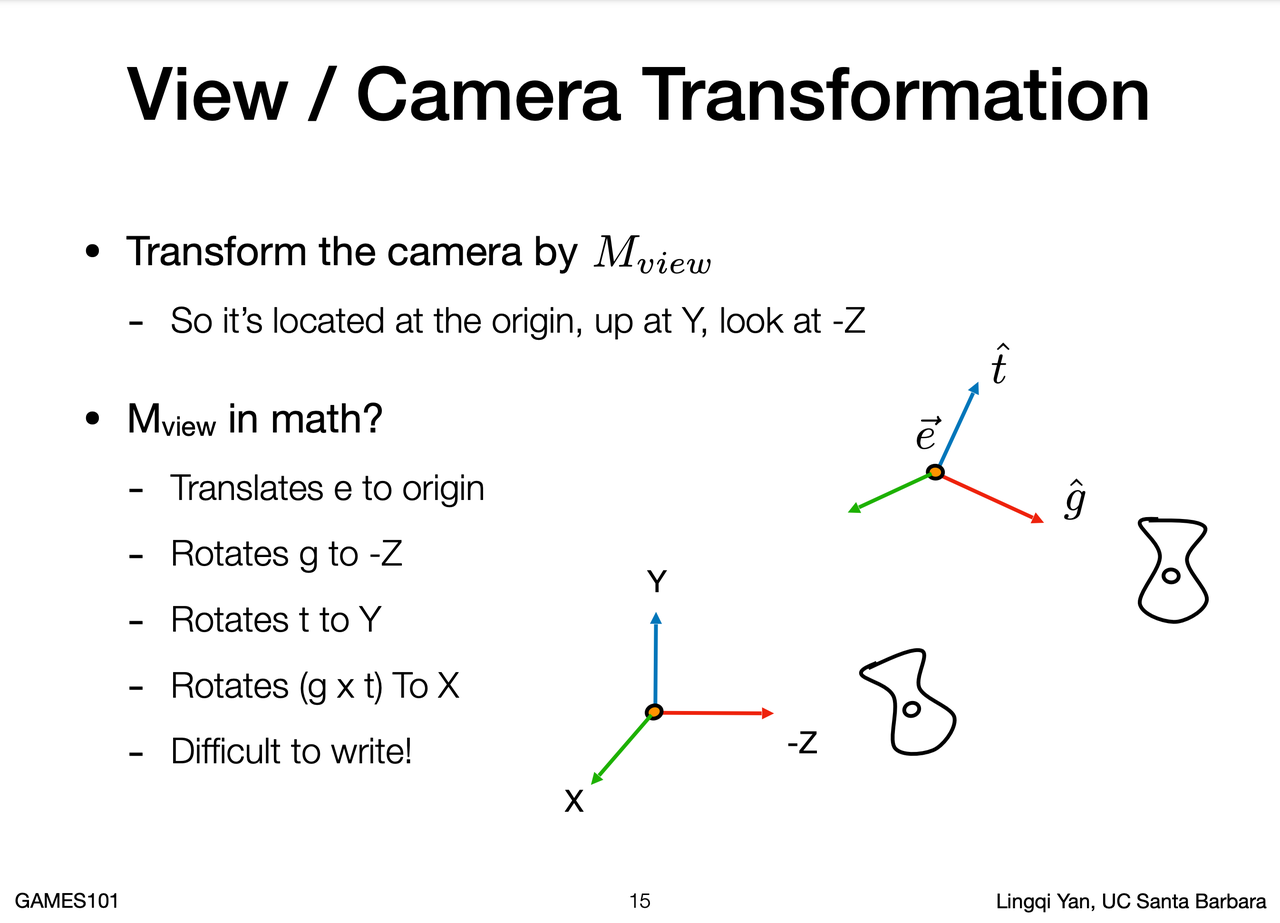
引用自: https://sites.cs.ucsb.edu/~lingqi/teaching/resources/GAMES101_Lecture_04.pdf

imgimg

抬高摄像机的高度

imgimgimg

imgimgimg

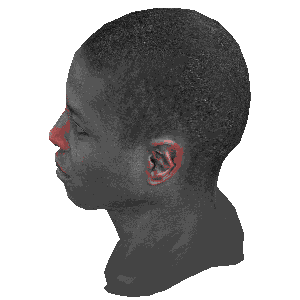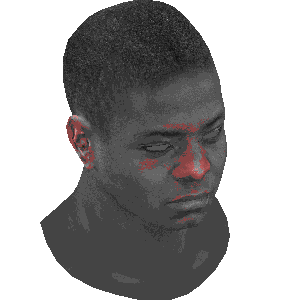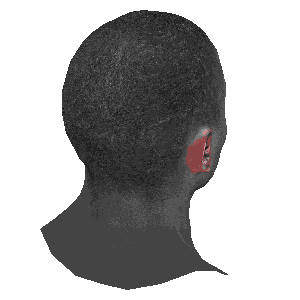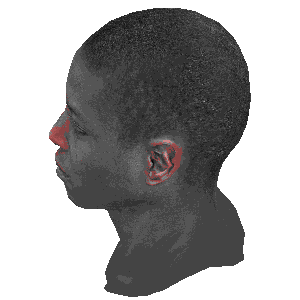
旋转的对比

imgimgimg

imgimgimg

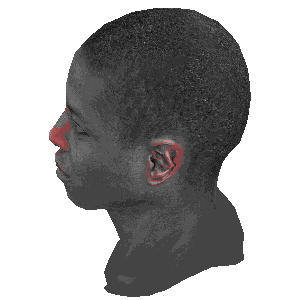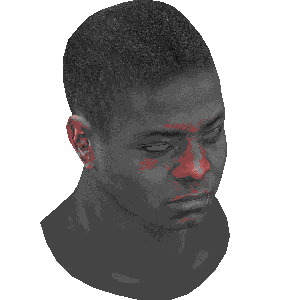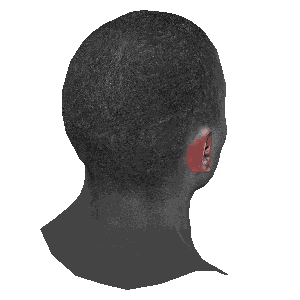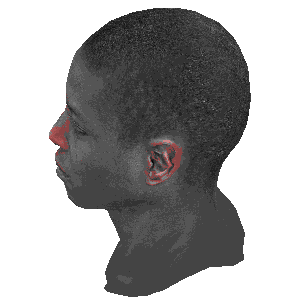
注:

左图: 模型自身旋转

中图: 摄像机围绕模型旋转

右图: 摄像机俯视模型旋转

正交/透视

img

imgimgimg

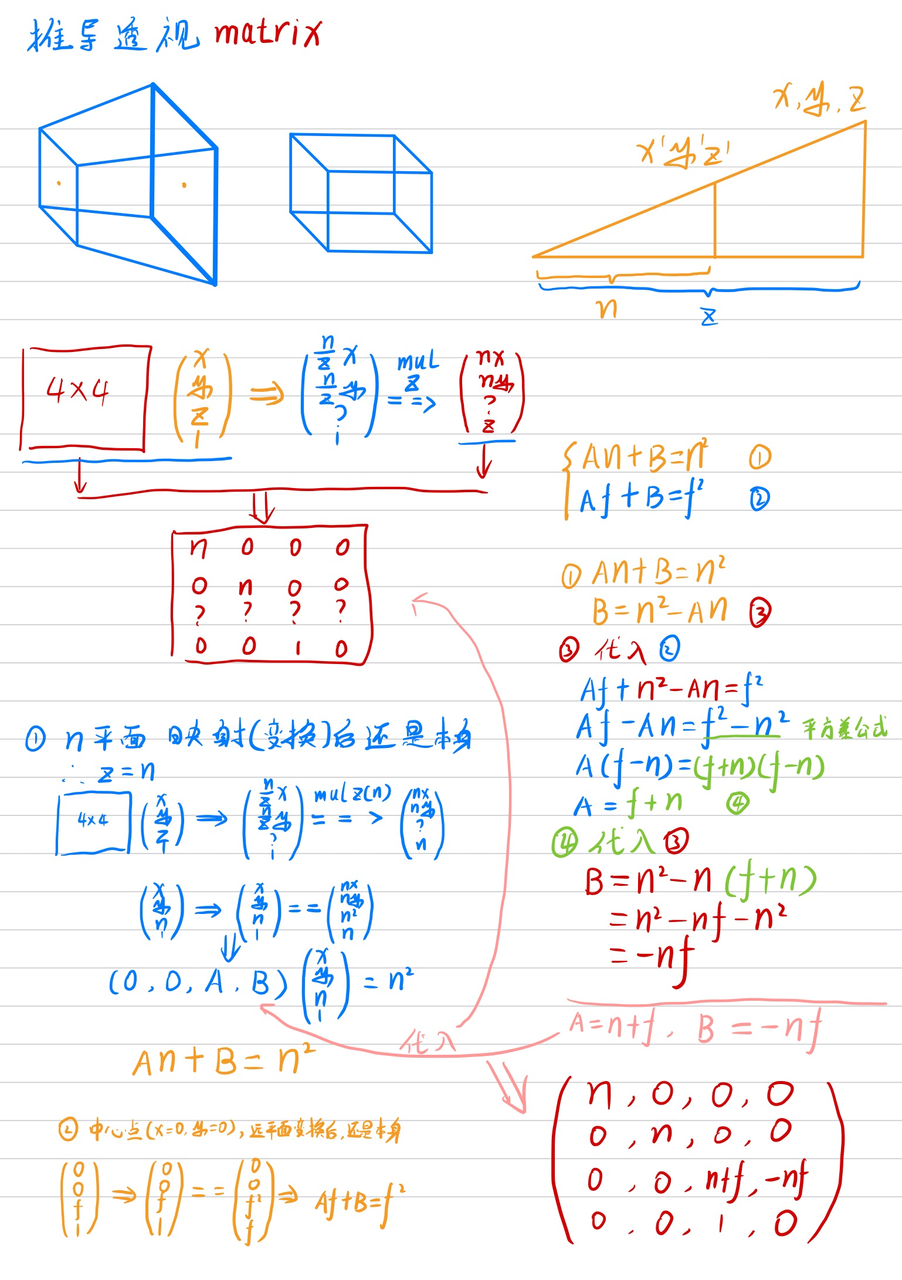
透视矩阵:

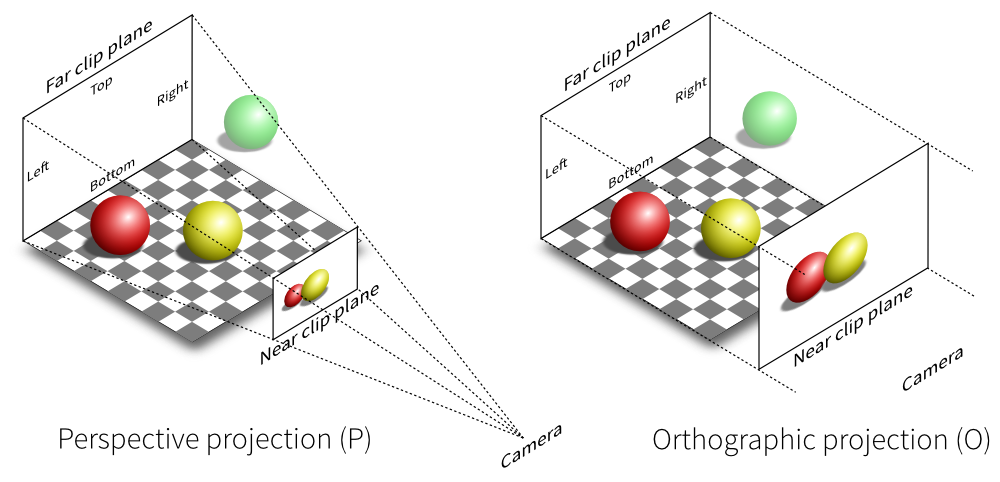
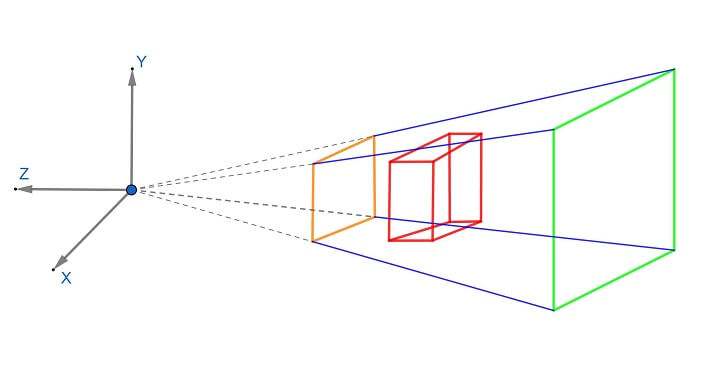
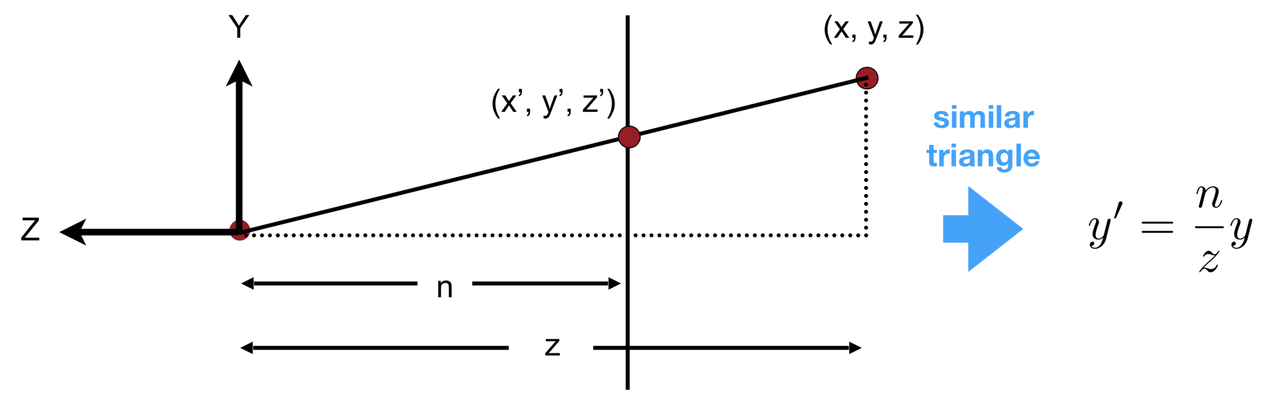
透视矩阵[近大远小]

imgimgimg

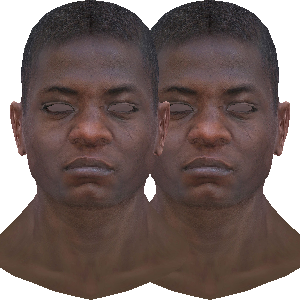
注:

左图: 正交投影

中图: 透视投影

左图和右图, 模型摆放位置是一样的

右图: 透视投影, 修改模型位置的动画

透视修正[重心坐标问题]

img

我们会发现 地板纹理 稍微有点问题, 因为光栅化计算深度插值的时候

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
v0, v1, v2 := 三角形的三个顶点坐标

// 计算重心坐标 alpha, beta, gamma
a, b, c := ma.Barycentric(
   // tri
   x0, y0, x1, y1, x2, y2,
   x,
   y)
// 判断是否在三角形内
if a < 0 || b < 0 || c < 0 {
   continue
}

z := v0.Z()*a + v1.Z()*b + v2.Z()*c

// UV 坐标 0, 0 在左下角
ux := int((a*uv0.X() + b*uv1.X() + c*uv2.X()) * float64(meta.MaxX))
vy := meta.MaxY - int((a*uv0.Y()+b*uv1.Y()+c*uv2.Y())*float64(meta.MaxY))

at := meta.At(ux, vy)

rr, gg, bb, aa := at.RGBA()
screen.SetColor(x, y, uint8(rr), uint8(gg), uint8(bb), uint8(aa), z)

示意图:

img

对比正交投影和透视投影中红色线段和蓝色线段对应的比例值

img

举例: 线段 AB, 投影到 A'B', A'B'的中心是 x=0 的位置, 但是映射到 AB 中, 并不是中心点, 所以插值后得到了一个错误的结果

矫正透视

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
// 计算重心坐标 alpha, beta, gamma
a, b, c := ma.Barycentric(
   // tri
   x0, y0, x1, y1, x2, y2,
   x,
   y)

// 判断是否在三角形内
if a < 0 || b < 0 || c < 0 {
   continue
}

// 修正透视变形的alpha, beta, gamma
// 1 / z = (1/z1 * alpha) + (1/z2 * beta) + (1/z3 * gamma)
uz := 1/v0.Z()*a + 1/v1.Z()*b + 1/v2.Z()*c
z := 1 / uz

a = a / v0.Z() * z
b = b / v1.Z() * z
c = c / v2.Z() * z

// UV 坐标 0, 0 在左下角
ux := int((a*uv0.X() + b*uv1.X() + c*uv2.X()) * float64(meta.MaxX))
vy := meta.MaxY - int((a*uv0.Y()+b*uv1.Y()+c*uv2.Y())*float64(meta.MaxY))
at := meta.At(ux, vy)
rr, gg, bb, aa := at.RGBA()
screen.SetColor(x, y, uint8(rr), uint8(gg), uint8(bb), uint8(aa), z)

矫正结果对比图

imgimg

成果:

img